贪心算法
简介
1、贪心策略,也称为贪婪策略。
每一步都采取当前状态下最优的选择(局部最优解),从而希望推导出全局最优解。
2、贪心的应用:
哈夫曼树
最小生成树算法:Prim、Kruskal
最短路径算法:Dijkstra
练习-最优装载问题(加勒比海盗)

贪心策略:每次选择最轻的上去(局部最优)
练习-零钱兑换

贪心策略:每次最优选择最大的(每次最优选择)
结果不一定全局最优。
练习-01背包

贪心策略:
1、优先价值(价值最大)
2、优先重量(重量最轻)
3、优先价值密度(价值/重量)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| + 实现
+ 准备
+ 物品类(价值、重量、价值密度)
+ 物品数组(sort:根据价值密度排序!!!)
+ 总重量、当前重量、总价值、装入物品list
+ 遍历物品数组
+ 装入物品(更新背包重量、价值、物品等)
+ 结束条件:装满
+ 动态规划:严谨做法
+ 贪心算法很多时候作为辅助(直接用不一定是最优的)!!!
+ 哈夫曼树
+ 贪心策略:每次选择最小的两个作为子节点!!!(放到最下面)
+ 保证距离远的权值小,权值大的距离进,实现最终结果小
+ 最小生成树
+ 普利姆(选路径小的相邻节点)、克鲁斯卡尔(选边,连成树)
+ 贪心策略:每次选择最小的边!!!(在生成树的前提下)
+ 最短路径
+ 克鲁斯卡尔(到每个节点最短的距离)
+ 贪心策略:找到最短路径!!!
|
递归
简介
递归:函数(方法)直接或间接调用自身。
栈空间:

拆解问题:同类型小问题
1、把规模大的问题变成规模较小的同类型问题
2、由最小规模问题的解得出较大规模问题的解
3、很多链表、二叉树相关的问题都可以使用递归来解决
- 因为链表、二叉树本身就是递归的结构(链表中包含链表,二叉树中包含二叉树)

使用
1
2
3
4
5
6
| + 使用套路
+ 函数功能
+ 原问题和子问题的关系
+ f(n)和f(n-1)
+ 结束条件
+ 什么情况下直接得出解
|

练习-斐波那契数列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| + 斐波那契数列
+ 结束条件:n<2
+ 递归:两个函数之和
+ 时间复杂度较大
+ 调用过程
+ 重复计算
+ 自顶向下的调用过程
+ 优化1
+ 数组存放计算过的结果(临时缓存)
+ 避免重复计算
+ list[i]放斐波那契第i位的结果
+ 简易缓存
+ 若缓存不存在,则计算
+ 若存在则直接返回
+ 优化2
+ 去除递归
+ 遍历填数组即可
+ 优化3
+ 每次运算只需用到数组中的两个元素
+ 滚动数组
+ 减少空间利用
+ 取模(&)效率更高、求余
+ 优化4
+ 两个int保存数据
+ 双指针
+ 优化5
+ 公式
|
递归转非递归
100%可以转非递归。
模拟栈。

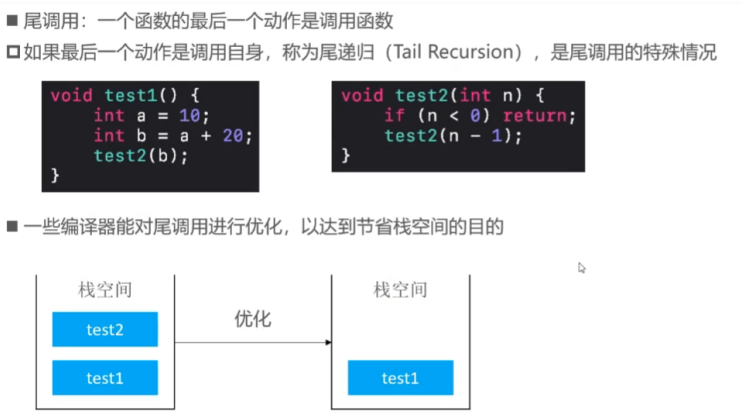
尾调用
最后一个动作是调用自身。

回溯
选择不同的岔路口来通往目的地。很适合递归。

分治算法
简介
1、分治,也就是分而治之。
- 将原问题分解成若干个规模较小的子问题(子问题和原问题的结构一样,只是规模不一样)
- 子问题又不断分解成规模更小的子问题,直到不能再分解(直到可以轻易计算出子问题的解)
- 利用子问题的解推导出原问题的解
因此,分治策略非常适合用递归
2、子问题相互独立——分治
子问题有关系——动态规划
3、应用:
快排(不断分两个子问题)
归并(分开排序)
Karatsuba算法(大数乘法)
4、分治策略:
分成子问题
合并子问题
练习-最大子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
| + 暴力穷举(所有区间):
+ 双指针划子序列区间
+ 暴力优化:
+ 利用上一次sum统计和
+ 分治
+ 若在mid中间(左右延伸)
+ 从mid加到左边,统计max
+ 从mid加到右边,统计max
+ 若在两边(取最大值)
+ 递归mid,begin
+ 递归mid,end
+ 从三者取最大值
+ 类似归并排序
|

练习-大数乘法
字符串一个一个相乘,一个一个相加

动态规划
简介
1、求解最优化问题
2、通常的使用套路(一步一步优化)
暴力递归(自顶向下,出现了重叠子问题)
记忆化搜索(自顶向下)
递推(自底向上)
练习-找零钱

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| + dp(i):凑到i最少硬币数
+ 状态转移方程
+ 考虑所有情况
+ 每次选择都有四种情况
+ 暴力递归
+ 问题
+ 自顶向下
+ 子问题重复
+ 记忆化搜索(临时缓存数组)
+ 递归时携带数组(边界等写入数组)
+ 问题
+ 自顶向下
+ 防止坐标越界
+ 动态规划!!!
+ 从第一个值往后推!!!(每个值都计算)
+ 后面的值借助前面的结果!!!
+ 所有的情况考虑进去
+ 自底向上递推
+ 求出方案所选硬币
+ 借助数组记录(arr[n]:总价为n,最后选的硬币)!!!
+ 若是最小值,修改数组(记录为本次选的硬币)
+ 遍历查找数组
+ 根据数组的值(选的硬币)确定前面的索引
+ 用数组存储硬币面值
|

常规流程
1
2
3
4
5
6
7
8
9
10
11
12
13
| + 动态规划
+ 定义状态(状态是原问题、子问题的解!!!)
+ dp[i]的含义等
+ 设置初始状态(边界)
+ dp[0]的值等
+ 确定状态转移方程
+ 确定dp[i]和dp[i-1]的关系等!!!
+ 题目特点
+ 最优子结构
+ 求解子问题的最优解,可以得到原问题的最优解
+ 无后效性!!!
+ 后面状态的演变不受前面的影响(未来与过去无关)
+ 推导状态只关心前面状态的值,不关心推导过程(只关心值:状态转移方程!!!)
|
练习-最大连续子序列和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| + 1、状态定义
+ dp[i]:以nums[i]结尾的最大连续子序列的和
+ 2、初始条件(边界:底层、最前面的值)
+ dp[0] = num[0]
+ 3、状态转移方程(由前面值推出来,后面推导与前面无关)
+ 若前面的最大子序列大于0,则加上末尾
+ 若前面最大小于0,只取末尾
+ 步骤
+ dp[i]
+ dp[0](前推后最底层)
+ 遍历dp(转移条件!!!)
+ 记录max
+ 求dp(n)只关心前面的dp(n-1),更前面的不关心,且没有作用了
+ 优化
+ 只用一个空间(后面的覆盖前面的值)
|

练习-最长上升子序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| + 求最大递增长度(非连续)
+ 解法1:动态规划
+ 状态定义 dp[i]以num[i]结尾的长度
+ 初始状态
+ 每个dp[i]为1
+ 状态转移方程
+ 遍历前面所有dp[j]
+ 若大于num[j],则dp[i] = dp[j] + 1
+ 若小于,跳过
+ 解法2:二分搜索★
+ 遍历数组
+ 若某一牌顶元素大于当前,放到其牌顶
+ 最终牌堆数量就是最长上升子序列长度
+ 原理
+ 保证从左往右,牌顶的大小一定是从小到大的!!!
+ 大的数(大于牌顶)往右移
+ 小的数(大于之前的牌顶,小于之后的牌顶)放到合适的前面合适的位置
+ 牌堆数组
+ 遍历每个元素时遍历牌堆数组,判断、赋值即可
+ 优化
+ 二分查找(数组有序),找到合适牌堆
|



练习-最长公共子序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| + 最长公共子序列(可以不连续)
+ 状态定义
+ dp(i,j) 前i个和前j个 公共子序列最大长度
+ 初始化
+ dp i 0 、dp j 0 初始值均为0
+ 状态转移方程
+ 如果i j最后一个元素相等,则dp(i-1,j-1) + 1
+ 如果不相等,最后一位元素对方前面元素是否有子序列
+ i-1和j的公共子序列、i 和 j-1的公共子序列 的最大值
+ 状态转移方程
+ 总之最后一个dp(i,j) 或者dp(i)
+ 要由前面的推出来i-1,j-1等之类的
+ 必须到考虑所有情况
+ 本次dp i j
+ 往前推 i-1,j-1,可以比较最后一位,若相等则构成子序列,直接+1
+ 若等于的情况,还不能确定是否有子序列
+ 最后一位往前继续比较
+ 则可以拿两个的最后一位分别和对面的前面进行比较
+ 实现
+ 递归解决
+ 结束条件(i=0,j=0)
+ 若相等,直接+1
+ 若不相等,获取最大值(i-1,j和i,j-1两个公共子序列,是否有构成新的序列)
+ 动态规划
+ 保证表格的每个格子都能由前面推出来
+ 一个格子一个格子推导
+ 一个格子只跟前面三个格子有关
+ 滚动数组
+ 一维数组(记住一行数据即可!!!)
+ 三个变量 ×
+ 表是一行一行计算的,并非斜着计算
+ 使用一维数组,需要提前保留左上角的值,否则被下面的覆盖
+ 计算左边的数之前,保留左上角的值
+ cur保存上面的值,给下次使用(当做左上角)
+ 优化
+ 使用长度小的作为一维数组
|


练习-最长公共子串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| + 动态规划
+ 状态定义:dp(i,j) 以i-1、j-1结尾的长度
+ 不存在则为0
+ 状态初始化
+ (i,0)、(j,0)均为0
+ 状态转移方程
+ 若i-1 == j-1,dp ij = dp i-1,j-1 + 1
+ 下一个两个字符相等
+ 若不相等,则为0(结尾不相等则为0)
+ 结果:max(dp i j )
+ 每一行进行遍历
+ 实现
+ 画表,容易理解流程,配合参数
+ 格子由左上角推得
+ 一维数组优化
+ 保留一行的左上角
+ 先保留上面,作为下一个的左上角
|


练习-01背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| + 动态规划
+ 状态定义
+ dp(i,j) 前i件物品,承重为j的可以选的最大价值
+ 状态初始化
+ i,0 、j,0 为0
+ 状态转移方程
+ 目标放在最后一件物品选还是不选:0/1
+ 如果j<weights[i],无法选
+ 则最后选择:dp(i,j) = dp(i-1,j)
+ 如果可以选
+ 如果最后一件物品不选,dp(i,j) = dp(i-1,j)
+ 如果选最后一件,dp(i,j) = dp(i-1,j-weights[i-1]) + values[i-1]
+ 则最后选择:dp(i,j) = max{ i 件商品0/1}
+ 实现
+ 一行一行计算
+ 一维数组优化
+ 每行从右往左算(左右不依赖,只依赖上面、左上的某一个值)
|

01背包-恰好装满:
1
2
3
4
5
| + 初始状态
+ dp(i,0) = 0 dp(0,j) = 负无穷
+ 必须从已经凑齐的格子过来(非负无穷),且下一个重量必须也凑齐(正数)
+ 才能计算出正数
+ 前面已经凑齐(只要值),只要这次凑齐就行
|

总结
1、步骤
定义状态(状态是原问题、子问题的解):比如定义 dp(i) 的含义
设置初始状态(边界)比如设置 dp(0) 的值
确定状态转移方程:比如确定 dp(i) 和 dp(i – 1) 的关系
2、可以用动态规划来解决的问题,通常具备2个特点。
最优子结构(最优化原理)
无后效性
串
简介
1、字符串 thank 的前缀(prefix)、真前缀(proper prefix)、后缀(suffix)、真后缀(proper suffix)
2、串匹配算法
蛮力(Brute Force)
KMP
Boyer-Moore
Karp-Rabin
Sunday
3、tlen 代表文本串 text 的长度,plen 代表模式串 pattern 的长度
暴力1
1
2
3
4
5
6
7
8
9
10
11
12
13
| + 实现
+ 循环 pi ti < plen tlen 有一个成立
+ 匹配成功
+ pi++
+ ti++
+ 匹配失败
+ ti -= pi - 1
+ pi = 0
+ true(pi == plen)
+ 优化
+ t 后面长度小于 p的长度
+ 没有必要比较了,直接失败
+ ti - pi <= tlen - plen
|


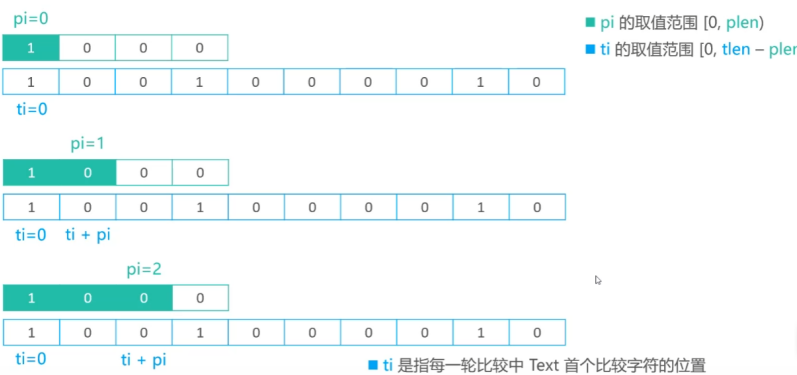
暴力2
ti含义:每一轮比较中,文本串首个比较字符的位置
1
2
3
4
5
6
7
8
9
| + 实现
+ 双循环 ti、pi
+ 匹配成功
+ pi++
+ 匹配失败
+ pi = 0
+ ti++
+ pi == plen
+ true
|

暴力性能分析

KMP算法
next表的使用:
1、KMP会预先根据pattern生成一张next表
2、在哪个地方失败,pi设为next[]相应的值
3、ti不变


得到next表


优化

性能分析

BM算法

RK算法

Sunday算法





















































